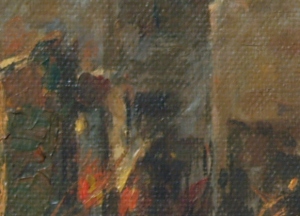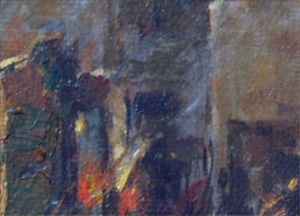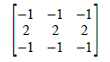Basic Video Processing

In our final activity, I took a video of a moving object and tried to extract its position frame by frame to derive a physical variable. The object I used with my group mate Ryan is a black basketball dropped from a certain height:

The above animation is slower than the real kinematic event. First, I extracted each frame from the video using the application Free Video to JPG Converter. Then, I tried to extract the ball from the image using Non-Parametric Estimation or Histogram backprojection (Image Segmentation). This is done by selecting a region of interest, taking its histogram in normalized chromaticity coordinates, and then backprojecting from the histogram to acquire the segmented image. I cropped a part of the ball in the image to use as a region of interest:

After cropping each frame to get a part where the ball appears, I segmented each frame individually, and got:

We can see that the ball was not successfully extracted. This is because of the white lines around the ball and some parts of the background that are also dark, which the segmentation process selects to be similar to the region of interest. I tried to get a clearer image of the ball using a closing morphological operator. Using a structure element with a radius of 20 pixels, I got:

We can see that the ball looks solid and filled for most frames, but it no longer looks like a circle. It is hard to apply color segmentation and morphological operations on our video to extract the ball because the color of the ball isn’t the same all throughout its body and because some objects in the background do not have high contrast with the ball.

Since these methods cannot work, I tried to extract the ball by converting the image to grayscale and do a simple segmentation by threshold (Image Segmentation). This was done by simply selecting pixel values greater than a threshold value of 50 and turning these values to 1, while turning all other values to 0. I got the result:

This looks better than the previous segmented images. From these processed frames, I tried to calculate the acceleration of gravity. For each frame, I calculated the y-coordinate of the centroid of the ball by taking the mean of all pixel locations of the extracted ball in the vertical axis. Before taking the video, I measured the length of the gray rectangle on the right side of the ball so I can convert a number of pixels to physical units.  I got a measurement of 66 cm  for 314 pixels and got a conversion value of 0.21 cm/pixel. Using this, I calculated the physical position of the ball in meters from the centroid y-coordinates:

I calculated the time difference for each frame from the video frame rate of 59 frames per second. The time between each frame is then just 1/59 seconds. I took the derivative of the positions to get the velocity of the ball, and got:

We can see that it almost looks linear, which is expected since the ball is supposed to have a constant acceleration, which is the acceleration due to gravity. I calculated the slope of the velocity versus time plot and got a value of 10.32 m/s^2 which yields a 5.20% error with the known value of acceleration due to gravity of 9.81 m/s^2.  This error could be due to the white lines around the ball which can shift the centroid upwards.

Since I needed to resort to segmentation by threshold instead of using color segmentation, I’ll rate myself with 9/10. The results could have been better and color segmentation would have been applicable if we had a video with a solid colored object all throughout and a background with high contrast.

I’d like to thank Dr. Soriano for all the fun activities in our class this semester. I enjoyed all activities and I’m sure my classmates did as well. I feel relieved and at the same time sad, but at last, we’re finished with all activities:

 

Reference:

M. Soriano, “A9 – Basic Video Processing,” Applied Physics 186, National Institute of Physics, 2015.

 

 

 

Morphological Operations

In this activity the aim is to understand and apply morphological operations, which are operations that affects an image’s shape, to enhance an image and extract information from it.

First, I apply dilation and erosion on a set of images. The dilation of a shape A by a structure element B is defined as:

It includes all translations z‘s of a reflected shape B such that it has an intersection with the shape A.  It expands A in the shape of B [1]. Erosion works in the opposite way and is defined by:

These are translations z’s of B such that it is contained in A. It reduces A in the shape of B [1]. I tried to predict the resulting dilation and erosion of different shapes by hand on graphing paper:

The objects are in the left most side, followed by the structure element, the erosion, and the dilation. Using the same shapes and structure elements, I checked the the correct results in Scilab using the IPD toolbox. I used the functions ErodeImage and DilateImage. I got the results:

In my predictions, I made a few mistakes with the erosion and dilation of the hollow square with the last structure element. Using Scilab is easier and faster because mistakes can easily be made when manually checking each pixel.

Next, I tried to apply morphological operations on images of circles:

We can imagine that these circles are cells in an absorbing medium. I tried to find a best estimate of the size of normal cells from the left picture, and then isolate the abnormal sized cells in the right picture.

First, I divided the left picture into 256 x 256 sized subimages. Here is one subimage:

After looking at its histogram to estimate the pixel value of the background, I binarized the image using a threshold:

ResultImage = Image > 200

This resulted in:

The image is still dirty because of some isolated pixels and small holes in the cell. The morphological operators close, open, and tophat, which utilize dilation and erosion, can be used to clean images such as this [2]. They are implemented in the IPD toolbox with the functions: CloseImage, OpenImage, and TopHat. Using a circle with a radius of 10 pixels as a structure element, the resulting image using close, open, and tophat are:

          

To clean the image, the opening operator is the most appropriate operator to be used. This operator removes light objects and retains dark objects where the structure element does not fit. After cleaning all the subimages by thresholding and opening, I got:

Next, I identified each blob in the above image using the function SearchBlobs. I then calculated the area of each blob and at the same time produced a histogram of the areas. This was done using the lines:

BlobImage = SearchBlobs(finalimage);
[sizes, bins] = CreateSizeHistogram(BlobImage);

This resulted with the histogram:

Majority of the blobs are found within the bins 375 to 598. These are the areas of the normal sized cells. I calculated the mean and standard deviation of these areas and acquired the best estimate area: 507.1 51.2.

Then, I tried to isolate the abnormally large cells in the other picture. After cleaning the image using the same method, I filtered out blobs that are smaller than the largest value of the best estimate, 558.3, and are smaller than the area of blobs made of touching cells. I got the latter area by looking at the histogram of the blob areas. I implemented the filter using the line:

FilteredImage = FilterBySize(BlobImage, ave+std, 1050);

where ave + std results in the largest value of the best estimate. This resulted in:

There are still some normal sized cells that were not eliminated. Most of them are made of touching cells. These can be eliminated by opening the image again, but now using a larger structure element. Compared with the original image, this resulted in:

     

Using the best estimate of the area eliminated most of the normal sized cells, but a final touch of opening the image again completely isolated the abnormally large cells.

Since I was able to demonstrate the dilation and erosion of different shapes with different structure elements, and apply morphological operations to isolate distinct shapes in an image, I rate my self with 10/10. Thanks to my classmate Jk for helping me understand the SearchBlobs function and in creating a histogram.

References:

1. M. Soriano, “A8 – Morphological Operations,” Applied Physics 186, National Institute of Physics, 2014.
2. opencv dev team, “More Morphology Operations,” OpenCV 2.4.12.0 documentation, 2014. Retrieved from: http://docs.opencv.org/2.4/doc/tutorials/imgproc/opening_closing_hats/opening_closing_hats.html at 26 November, 2015.

 

Image Segmentation

The aim in this activity is to segment images by picking a region of interest (ROI) and then processing the images based on features unique to the ROI.

For grayscale images where the ROI has a distinct grayscale range, segmentation can easily be done by using thresholding. For example, lets take the image:

Using Scilab, the grayscale histogram of the image read as I can be computed and plotted using the lines [1]:

[count, cells] = imhist(I, 256);
plot (cells, count);

This results in:

The large peak corresponds to the background pixels which are lighter than the text. To segment the text, we can assume that using a threshold of 125 can be used since it is less than and far from the pixel values of the peak. This can be implemented using the lines [1]:

threshold = 125;
BW = I < threshold;

This results in:

where only the pixels having values less than the threshold of 125 are colored white. Using threshold values of 50, 100, 150, and 200, (left to right, up to down) I got:

We can see that using a lower threshold than needed will segment fewer details while using a higher threshold than needed will include too much unwanted details in the segmented image.

The problem of segmentation for colored images is more complicated. ROI’s that have unique features in a colored image might not be distinct after converting the image to grayscale [1]. Also, when segmenting images that have 3D objects, the variation in shading must be considered. Because of this, it is better to represent colors using the normalized chromaticity coordinates or NCC [1].

The NCC can be computed using the equation:

where . Since b is dependent on r and g, the chromaticity can be represented by using just the two coordinates r and g. I represents the brightness information [1]. The normalized chromaticity space is then shown in the plot:

where the x-axis is r and the y-axis is g [1].

A. Parametric Estimation

Segmentation can be done by calculating the probability that a pixel belongs to the color distribution of the ROI. To do this, we can crop a subregion of the ROI and compute its histogram. When normalized by the number of pixels, the histogram is already the probability distribution function (PDF) of the color. Assuming a Gaussian distribution for r and g, independently, of the cropped region, the means , , and standard deviations ,  can be computed [1]. The probability is then computed using the equation:

A similar equation can be used for p(g). The joint probability is then the product of p(r) and p(g) and can be plotted to produce a segmented image [1].

B. Non-Parametric Estimation

Histogram backprojection is a method where a pixel value in the image is given a value equal to its histogram value in the normalized chromaticity space. This can be used to segment images by manually looking up the histogram values. A 2D Histogram can be obtained by converting the r and g values to integers and binning the image values to a matrix. This can be implemented using the code [1]:

BINS = 180;
rint = round (r*(BINS-1) + 1);
gint = round (g*(BINS-1) + 1);
colors = gint(:) + (rint(:)-1)*BINS;
hist = zeros(BINS,BINS);
for row = 1:BINS
for col = 1:(BINS-row+1)
hist(row,col) = length( find(colors==( ((col + (row-1)*BINS)))));
end;
end;

where r and g are taken from the ROI. Then, the segmented image can be computed using the code [1]:

rint = round (r*(BINS-1) + 1);
gint = round (g*(BINS-1) + 1);
[x, y] = size(sub);
result = zeros(x, y);
for i = 1:x
for j = 1:y
result(i,j) = hist(rint(i,j), gint(i,j));
end;
end;

where r and g are taken from the subject image.

C. Results

The first image I segmented is a drawing of one of my favorite monsters from the game Monster Rancher, Mocchi:

souce: deviantart

The colors found on its head (green), lips (yellow), body (cream), and belly (cream) all appear solid. I cropped the following ROIs:

                  

for the four parts. After applying parametric estimation, I got (left to right, up to down):

We can see that the corresponding body parts of Mocchi, depending on the cropped ROI, were successfully segmented. After looking closely at the image, I saw that there are actually distortions near the black pixels (Mocchi’s edges). These distortions are the reason why the segmented images do not exactly follow Mocchi’s shape.

Next, I segmented an image of pick-up sticks:

source: choicesdomatter.org

First, I used an ROI from a green stick that has minimal shading variations:

Using parametric estimation, I got the following segmented image:

We can see that some areas are not segmented perfectly. These areas are those of really bright or really dark shading. Using an ROI from a stick with more shading variations:

I got:

We can see that the green sticks are clearly identified by the white pixels, however, other areas are no longer black. This is because the features of the new ROI are no longer unique to just the green sticks. For the other colors, I will continue with using ROIs taken from sticks with minimal shading variations:

                 

I will also apply non-parametric estimation. First, I plotted the histogram of the ROIs, respectively:

If we look at the plot of the normalized chromaticity space again, we can see that the location of the peaks are located inside the corresponding expected regions. Therefore we can say that the histograms are correct. For the green, red, yellow, and blue ROIs, respectively, I got a segmented image using parametric estimation (left) and non-parametric (right) estimation:

green:

red:

yellow:

blue:

We can see that using parametric estimation segments the corresponding pick-up sticks more accurately than using non-parametric estimation. For this case, using non-parametric estimation identifies fewer pixels to be similar to the ROI since it directly uses the histogram instead of using a probability distribution. Therefore it is not suitable for use when segmenting images with objects that have really small widths such as these pick-up sticks. After using non-parametric estimation on the image of Mocchi using the same ROIs shown in the first part of the results, I got:

We can see that the segmentation is still successful since the parts corresponding to the different ROIs are large enough.

This activity was fun because I can instantly be gratified by the results since they can be confirmed by just looking at the segmented images.

Since I was able to obtain all the required images, I will rate myself with 10/10. Also, thanks to John Kevin Sanchez, Ralph Aguinaldo, and Gio Jubilo for helping me in correcting my equations and understanding backprojection.

References:

1. M. Soriano, “A7 – Image Segmentation,” Applied Physics 186, National Institute of Physics, 2014.

Image Reference:

img-comment-fun

Properties and Applications of the 2D Fourier Transform

The aim in this activity is to investigate some more properties of the 2D Fourier Transform (FT) and to apply these properties in enhancing images.

A. Anamorphic property of FT of different 2D patterns

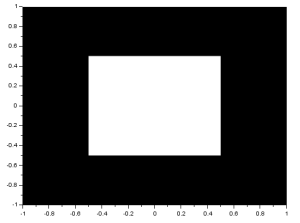
As we know, the FT space is in inverse dimension. Because of this, performing the FT on an image with an object that is wide in one axis will result in a narrow pattern in the spatial frequency axis [1]. As examples, I will show the FTs of different patterns. I implemented the FT in Scilab using the functions given in (Fourier Transform Model of Image Formation). For a tall rectangular aperture:

              

The FT is the image in the right. For a wide rectangular aperture:

               

We can see that the resulting rectangles in the y-axis for the wide rectangle are narrower than that of the tall rectangle. On the x-axis, we can see that the resulting rectangles are shorter for the tall rectangle. For two dots along the x-axis:

               

For two dots with a different separation distance:

               

We can see that the wider the space between the two dots is, the narrower the space between the peaks of the resulting sinusoid pattern (also, the higher the frequency).

B. Rotation Property of the Fourier Transform

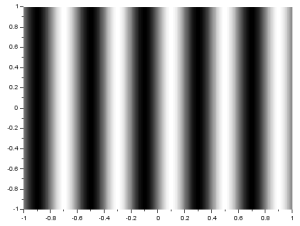
Next, I will investigate the rotation property of the 2D FT where rotating a sinusoid results in a rotated FT [1]. The following images are of sinusoids and their resulting FTs:

The generated matrices used for these images have negative values. Since digital images have no negative values, these sinusoids are not perfect. Because of this, we see multiple dots in the FTs although they were expected to have only two dots which identify the sinusoids’ frequency. Still, we can observe the anamorphic property of the FT. We can see that the resulting dots farther from the center are produced for sinusoids which have closer peaks. To correct the sinusoids, I applied a constant bias so that all values are positive. I got the resulting sinusoid and its FT:

           

Now we can see fewer dots. The central dot comes from the applied bias. Given a signal or pattern, we can measure its actual frequency by performing the FT and measuring the distance of the two dots from the center. After applying a non-constant bias (a very low frequency sinusoid) to the sinusoid, I got:

           

If we look closely, we can see two dots near the central dot. These dots represent the frequency of the non-constant bias. If it is known that the bias has a very low frequency, the frequency of the signal can still be measured using its FT.

After rotating the sinusoid, I got:

           

We can see that the resulting FT pattern rotated as well. Then, I created a pattern formed by adding a sinusoid along the x-axis and a sinusoid along the y-axis. Both sinusoids have the same frequency. I got:

           

As expected, there are four dots in the resulting FT pattern. Two dots placed on the x-axis and two dots placed on the y-axis. When i multilpy the two sinusoids instead, I get:

           

The product of two sinusoids along the same axis is given by the following equation [2]:

We can see that the product is equivalent to the difference of two sinusoids with frequencies formed from the difference and sum of the frequencies of the original sinusoids. This adding and subtracting of frequencies could be the reason for the position of the dots in the resulting FT.

Finally, I added multiple rotated sinusoids to the previous pattern and performed the FT. I got:

          

Looking closely, we can see dots around the central dot and they actually form a circle. These dots represent the frequency of the 10 rotated sinusoids that I used. This further proves that a rotated sinusoid also has a rotated FT.

C. Convolution Theorem Redux

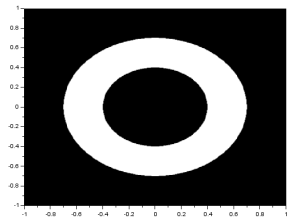
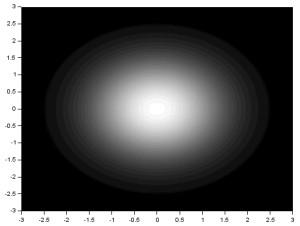
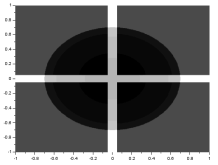
I performed the FT on an image with two circles along the x-axis:

           

We know that the FT of two dots is a sinusoid and that the FT of a circle is composed of rings. Noting that, we see that the resulting FT here resembles the product of the FT of two dots and the FT of a circle. I also performed the FT on an image with two squares and got:

           

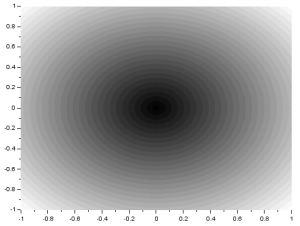
Again, the resulting FT looks like the product of the FT of two dots and the FT of a square. Using two Gaussians of different , I got:

We recall that the FT of a Gaussian is also a Gaussian. Again, the resulting FT looks like the product of the FT of two dots and the FT of a square. From the three previous results, we can observe that the inverse FT of the product of the FT of two dots and the FT of another pattern results in a replication of the pattern at the position of the dots. This, in fact, demonstrates the convolution theorem [1]:

A dot in a 2D image actually represents a dirac delta function. We know that the convolution of a dirac delta and a function f(t) replicates f(t) in the location of the dirac delta. Knowing this, we can apply it using an image containing dots and an image containing a distinct pattern. I convoluted a 3×3 pattern which forms a cross (x) with the following image:

and got:

We can see that if we invert x and y in the resulting image, the cross pattern will appear at the location of the points. The axes were inverted because quadrants are shifted when using the fft2() function in Scilab.

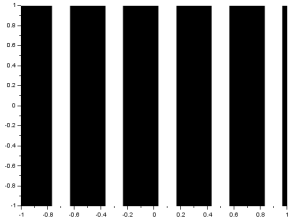
Next, I performed the FT on equally spaced dots, with a different spacing for each image:

The second batch of images are the resulting FTs for each corresponding image. For each FT, the sinusoids produced by the multiple dots must have accumulated to form dots with a different spacing. Again, we can observe the anamorphic property of the FT. Knowing the appearance of the FT’s of different patterns, such as this, can be used in constructing filters for image enhancement.

D. Fingerprint: Ridge Enhancement

Next, lets apply the convolution theorem to enhance images. I took an image of my fingerprint, turned it to grayscale, and binarized it.

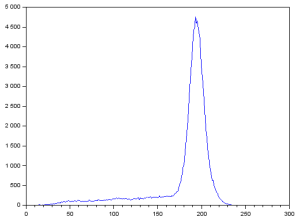
We can see that there are some areas with blotches and light areas. I took the FT of the grayscale image and got:

We can see that there is a distinct ring. This ring must represent the frequencies of the ridges of my fingerprint. Knowing this, I constructed the filter:

I multiplied this filter with the FT and performed an inverse FT. I got the resulting enhanced fingerprint and binarized it using the same threshold.

           

We can see that the ridges are now more distinct and the blotches have been reduced.

E. Lunar Landing Scanned Pictures: Line removal

I applied the same method to the image:

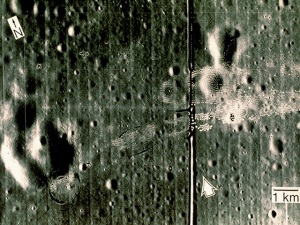
We can see that there are vertical lines throughout the image. It’s not obvious but there are also horizontal lines. I took its FT and got:

Looking closely we can see that there are several dots along the x and y axes. These must represent the frequencies of the vertical and horizontal lines. I constructed the following filter:

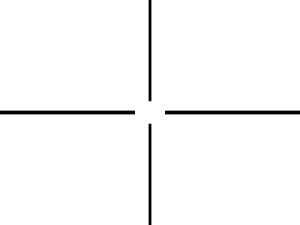
After doing the same thing as in part D, but instead on the RGB components, individually, and then forming the colored image again, I got:

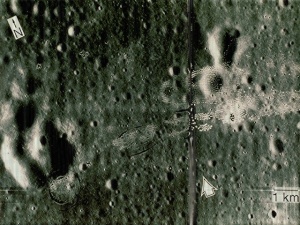
We can see that the vertical and horizontal lines have been removed.

F. Canvas Weave Modeling and Removal

For a final application, let’s look at the image:

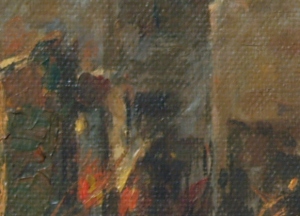
We can see the weave patterns of the canvas. I performed the FT on the image and got:

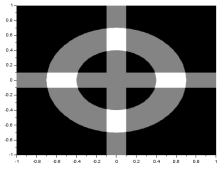
We can see some dots along the x and y axes and four more dots that form the corners of a rectangle. These dots must represent the frequencies of the weave patterns. I then constructed the filter:

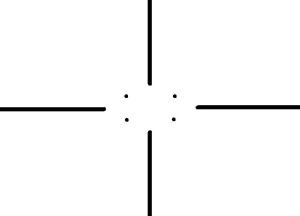
After applying the same method as in part E, I got:

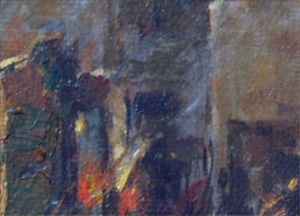
We can see that the presence of the weave patterns has been significantly reduced. To check the filter I used, I took the inverse FT of the filter’s inverse and got:

We can see that it resembles the weave pattern in the painting. Using the convolution theorem by multiplying the inverse of the FT of the pattern we want removed (the filter) with the FT of the image, and then taking the inverse FT is an easy way of enhancing images.

This activity was very long but was very fun to do especially when I actually tried to enhance images. Although there are many more applications in using the FT, I feel like this is some sort of culmination of all the practice done in the previous activity and even of the required study we did on the Fourier Transform in our math and physics subjects. Since I was able to produce all the required images, I will rate myself with 10/10.

References:

1. M. Soriano, “A6 – Properties and Applications of the 2D
   Fourier Transform,” Applied Physics 186, National Institute of Physics, 2014.
2. ” Table of Trigonometric Identities,” S.O.S Mathematics, 2015. Retrieved from: http://www.sosmath.com/trig/Trig5/tritacg5/trig5.html

Image Reference:

http://mrwgifs.com/squall-rinoa-zell-victory-poses-in-final-fantasy-8/

Fourier Transform Model of Image Formation

The aim in this activity is to familiarize with the use of the Fourier Transform to form images and some of its simple applications like template matching and edge detection.

The Fourier Transform

The Fourier Transform or FT is a linear transform that converts a signal that has dimensions of space into a signal in inverse space or spatial frequency. The FT of an image f(x,y) is given by the equation

where and  are the spatial frequencies along x and y [1].

The Fast Fourier Transform of FFT is an efficient implementation of the FT made by Cooley and Turkey. In Scilab, the FFT routine is called using the function fft2() for 2D signals [1].

I created an image of a circle:

In Scilab, I read the image using imread() and converted it to grayscale using mat2gray(). I performed the FT on the matrix using fft2() and got the resulting image:

The quadrants of this image still need to be shifted because the output of fft2() has interchanged quadrants [1]. After using fftshift(), I got the resulting image:

          

The image in the right is just a zoomed image. The resulting frequency pattern is formed of a small circle and concentric rings. This was the expected result for a circle image. If we consider the circle to be in the frequency domain, two points that have the same distance from the center will have an inverse FT that will be a sinusoid with a frequency given by the distance. Since the circle is made of many points with equal distance from the center, it will form multiple sinusoids with different orientations that will ultimately form concentric rings.

After applying fft2() twice on the image, i got the resulting image:

This is just similar to the original image but just slightly shifted. This is the result since applying the fft2() twice will just invert the image back to its original dimensions. If I take the real and imaginary parts, respectively, of the FT of the circle image, I get:

          

confirming that the FT is complex. I also created an image of the letter A:

After taking the FFT, shifted FFT, and applying the FFT twice, respectively, I got:

       

In the shifted FFT, the cross comes from the sides of the letter A and the vertical pattern in the center comes from the horizontal line of the letter A and its top. We can see that after applying the FFT twice, the resulting image is similar to the original. This time it is inverted because of the interchanged quadrants. Taking the real and imaginary parts of the image’s FT, I got:

           

FTs of Different Images

Next I will show images and their corresponding shifted FFTs. First for a sinusoid along x:

          

For this image, I first shifted the pixel values so that they are all positive. The resulting FT image is formed of 3 dots. The central dot is there because of the shifting of the image. This is similar to what happens when taking the FT of a voltage signal with an offset to have only positive values. The other dots represent the frequency of the sinusoid.

Then, for a double slit:

        

The left most image is just a zoomed image. Using the FT on the double slit simulates Young’s experiment that results in a diffraction pattern made of fringes when letting light pass through two apertures or slits.

Next, for an image of a square:

          

The resulting image is formed of a small square at the center and small rectangles formed on its sides. If I use a smaller square, I get:

          

We can see that the resulting frequency pattern became larger. This is because after applying the FT, small features become big and large features become small [2].

Lastly, for a 2D Gaussian bell curve:

           

The resulting FT is also a Gaussian curve. Like the square image, using a smaller Gaussian curve as the image will yield a larger FT.

Convolution and Simulation of an Imaging Device

Next I perform a convolution which is similar to a smearing of one function with another [1]. The convolution between two 2D functions f and g is given by:

The resulting function h will have properties taken from the two functions f and g. For an imaging system, the f can represent the object, g can represent the transfer function (e.g. finite size of lens), and h can represent the produced image [1]. Linear transformations obey the convolution theorem [1]:

meaning i can compute the result h by taking the inverse of the product of Fourier Transforms H.

I performed a convolution between an image of the letters “VIP” and an image of a circle:

          

I first took the FFT of the vip image and multiplied it to the matrix of the circle image since it is already in the Fourier plane [1]. Then I took the inverse FFT of the resulting product. For circles of radius 0.2, 0.4, 0.6, and 0.8, respectively, I got:

          

          

We can see that the resulting image becomes clearer as the radius of the circle is increased. This is a simulation of an imaging device where the circle represents the aperture. As expected, using a larger aperture results in a clearer image.

Correlation and Template Matching

The correlation between two 2-D functions f and g is given by the equation:

where the correlation p measures the degree of similarity between the two functions. It can also be calculated using the equation:

where P, F, and G are the FTs of p, f, and g and the asterisk stands for complex conjugation.

I took the correlation between the two images:

          

This was done by taking the product of the FT of the A image and the conjugate of the FT of the text image. The correlation image is then the inverse FFT of the product. The resulting output is:

We can see that only the parts where there is a letter A in the text image are clear while the other parts are blurry and unreadable.

Edge Detection

Edge detection was performed by convolving the VIP image with a 3×3 matrix pattern of an edge that has a total sum of zero. For example, a horizontal edge can be represented by the matrix [1]:

Convolving this with the VIP image resulted with the output:

We can see that the horizontal edges of the letters are more visible than the other parts of the letters. Using other edge patterns such as a vertical, diagonal, and spot pattern, respectively, resulted with:

        

We can see that depending on the edge pattern used, the edges with the same orientation with the pattern become more visible. Using a spot pattern, the edges of the letters on all orientations were detected.

This activity was fun because we had to generate a lot of images. Interestingly, the harder part of the activity for me was controlling the format of the images such as using mat2gray() on the output rather than the part where I apply the Fourer Transform or perform a convolution. With this problem I got some help from my classmates Martin Francis D. Bartolome and John Kevin Sanchez. Since I was able to generate all the required images, I will rate myself with 10/10.

References:

1. M. Soriano, “A5 – Fourier Transform Model of Image
   Formation, ” Applied Physics 186, National Institute of Physics, 2014.
2. F. Weinhaus, “ImageMagick v6 Examples — Fourier Transforms”, imagemagick.org, 2011. Retrieved from: http://www.imagemagick.org/Usage/fourier/
3. P. J. Bevel, “The Fourier Transform at Work: Young’s Experiment,” The Fourier Transform .com, 2010. Retrieved from:  http://www.thefouriertransform.com/applications/diffraction3.php

Length and Area Estimation

The aim in this activity is to calculate the area of images using Green’s Theorem and through morphological operations.

First, the area of regular geometric shapes was calculated. A circle and square were produced as in the activity Scilab Basics and was saved as an image using the imwrite() function from the SIVP Toolbox.

           

Using the edge() function, the edges of the shapes were obtained:

        

Then, pixel coordinates (x, y) of the edges were extracted using find() and were translated by subtracting the centroid. For these images the centroid is just the center of the image. Then, the angle θ = atan(y, x) was calculated for all the points of the edge. The (x, y) pairs were then sorted according to increasing θ. The sorted (x, y) pairs define the contour of the edge. This was implemented in Scilab using the lines:

while i < n,
    j = find(theta == theta_sorted(i));
    [r, s] = size(j);
    for k = 1:s
        xcon($+1) = x_e(j(k))
        ycon($+1) = y_e(j(k))
    end
    i = i + s
end

where (xcon, ycon) are the lists of x and y contour coordinates, (x_e, y_e) are the lists of x and y edge coordinates, theta is the list of angles and theta_sorted is the list of sorted angles. The for loop was necessary for the cases where there are more than 1 indices returned by the find() function.

Using Green’s theorem, the area of each shape was calculted using the formula [1]:

For the circle, an area of 17529 px² was calculated while the actual area is 17671 px². For the square, an area of 22465 px² was calculated while the actual area is 22500 px². The calculations yielded percent errors of 0.80% and 0.15% for the circle and square, respectively.

The same method was performed on the lot area of the Enchanted Kingdom theme park in Santa Rosa City, Laguna, Philippines. An image of the lot was obtained from google maps and was delineated usng GIMP 2.8:

        

The only difference in the method was that the centroid had to be calculated first since the shape of the lot is irregular. This was done by averaging the pixel locations of the part of the image occupied by the lot. The edge of the image was again obtained using the edge() function:

The area was then converted into actual units by measuring the pixels of the absolute scale shown in the Google map. The calculated area was 16.3 hectares while the actual lot area is 17 hectares [2]. This yields a percent error 4%.

Lastly, using the ImageJ application, a scanned image of my ID was analyzed:

Using the straight line tool, I drew a line along the shorter edge of the image. I also measured its actual distance using a ruler. Then, I set the scale using Analyze > Set Scale by entering the actual distance. Then I was able to measure the longer edge of the image using Analyze > Measure. The calculated length was 84.5 mm while the actual length was 86 mm. After selecting the whole image, its area was calculated using Measure. The resulting area was 4562 mm² while the actual area is 4644 mm². This yields a percent error of  1.7%. ImageJ uses morphological operations which are estimations done by counting pixels. We can see that it was successful in calculating lengths and areas with small errors.

I also used ImageJ to calculate the area of the delineated image of the Enchanted Kingdom lot. The calculated area was 16.99 h and confirms the credibility of the actual area taken from the source. Since all calculations have minimal errors, I am going to rate myself with 10/10. I had fun with programming the area calculation using Green’s Theorem especially with the challenging part for me which was the sorting of the coordinates according to increasing angle since I am still new to Scilab.

References:

1. M. Soriano, “A4 – Length and Area Estimation in Images,” Applied Physics 186, National Institute of Physics, 2014.
2. “Enchanted Kingdom,” Wikipedia. (en.wikipedia.org/wiki/Enchanted_Kingdom)

Scilab Basics

In this activity, the aim is to create a number of synthetic images as a practice for future testing of algorithms or simulations of optical phenomena in imaging systems.

Sample code written in Scilab that creates a circular aperture was given to us. The code produces the image:

This was performed by first creating two 2D arrays (X and Y) containing x and y coordinates ranging from -1 to 1 using the ndgrid() function. The number of x and y elements are set using the variables nx and ny respectively.  With the line:

r = sqrt(X.^2 + Y.^2);

A matrix r is created that contains circle radius values. The value of r(x,y) is equal to the radius of a circle centered at (0,0) whose edge lies on (X(x,y),Y(x,y)). The matrix r represents the radius values of circles with varying sizes centered at the origin. When plotted, the matrix r looks like:

Then, a zero matrix A with the same size as r was created. With the line:

A (find(abs(r)<0.5) ) = 1;

Indices where r < 0.5 are chosen and the value of A at these indices is changed to 1. This will form a circle with a radius equal to the value in matrix r which is closest to but less than 0.5. For high nx and ny, this will produce a radius which is approximately 0.5.

Other synthetic images can be made by varying A or r. To make a centered square aperture, I replaced last line above with:

A (find(abs(X)<0.5) ) = 1;
A (find(abs(Y)>0.5) ) = 0;

First, indices representing |x| < 0.5, the value of A is changed to 1. This will form a rectangle. The second line turns the image into a square by returning the values where |y| > 0.5 to 0. The resulting image is:

To produce a sinusoid along the x-direction or a corrugated roof, r was simply adjusted to:

r= sin(X*5*%pi);

and was plotted.  The resulting image is:

To produce grating along x, I simply added the line:

A (find(r>0.5) ) = 1;

to the code for the sinusoid. This is a discrete version of the sinusoid since certain values of r are changed to just either 1 or 0. The result is:

To produce an annulus, I simply adjusted the original code to produce two circles of different size. One circle made of 1 values and the other made of 0 values. The resulting image is:

To create a circular aperture with Gaussian transparency, the range was changed to -3 to 3 and the matrix A in the original code was replaced with:

G = 1/sqrt(2*%pi)*exp(-(r.^2)/2);
G (find(r>2.5) ) = 0;

The first line is simply the equation for the Gaussian Distribution. The second line blackens the area outside of the circle with radius 0.8. The range was changed so that more shades of gray are used. The result is:

An ellipse can be made by simply multiplying either X or Y in the original code by a constant with a magnitude less than 1.  The result is:

A cross can be made by adjusting the code for the square image. Replacing the lines assigning values to A with:

A (find(abs(X)<0.2) ) = 1;
A (find(abs(Y)<0.2) ) = 1;

forms the image:

Using the matrix for the cross image and adding it to the annulus matrix, subtracting the gauss matrix from it, and multiplying it to the circle matrix, the following images were formed:

             

Figuring out how to produce each image was fun and maybe being new to programming in Scilab made it even more fun. Even figuring out some new functions like find() was enjoyable. Since I have produced all the required images and explored the outcomes of combining matrices for different images, i would rate myself with a grade of 10.

                                          *ten tententenen ten tenenenenen ten ten ten teneeen

References:

M. Soriano, “A3 – Scilab Basics,” Applied Physics 186, National Institute of Physics, 2014.

Image References:

http://cuddlychriscrymsyn.tumblr.com/

Digital Scanning

The aim of this activity is to acquire the numerical values of a hand drawn plot using pixel values of its digital image.

The first thing I did, with the help of my classmates, was to find an old journal with a graph that is not digitally printed. I would say this was the hardest part of the activity. After a lot of searching, we finally found the journal entitled “The microbiological assay of amino acids in some Philippine legumes” by Nieves Portugal-Dayrit from the CS library. I chose a hand-drawn graph, photocopied it and then scanned it. This is the scanned image:

Next, I opened the image in GIMP 2.8. The first thing I did was correct for  rotations. To do this i selected a proper grid spacing by going to Image > Configure grid, and then showed the grid by going to View. Then I rotated the image using Tools > Transform Tools > Rotate to align the axes with the grid.

Now to relate image pixel location with the physical values in the plot, I first need to know how many pixels a single physical unit takes (pixels per unit). I moved the mouse over the tick marks of both the X and Y axis and noted the pixel locations x_p and y_p. I took the difference between pixel locations of adjacent tick marks, and took the average difference. The number of pixels a single physical unit takes can then be calculated by taking the average difference divided by the physical interval of the tick marks. For example, if the pixel locations for the tick marks in the X axis are x₁, x₂, x₃ and the physical interval is 2.5 (as in the image), the pixels per unit, say p_u, is then:

I also took note of the pixel locations of the origin x_0 and y_0. I found the p_u‘s to be 162.08 and 804.4 for the X and Y axes respectively. Since a single unit in the X axis spans 162.08 pixels, the physical value x = 1 must have an x_p equal to x₀ + 162.08. x = 2 must have an x_p equal to x₀ + 2(162.08) and so on:

Rearranging, we get:

The same also applies to values in the Y axis except the sign is changed because y_p = 0 at the top of the image:

Knowing the last two equations, I can simply take pixel locations of points in the curve and convert them to physical values. Using the mouse, I took pixel locations of 25 points, converted the locations to physical values, and plotted the values in Excel.

Here is the result:

I used the image of the plot as a background of the Excel plot area. The reconstructed graph very closely replicates the scanned graph. Because of this, I would rate myself 9/10 for the reconstruction.

The limitation in the method I used is using the mouse to find pixel locations. That isn’t very accurate since the curve line has a width which contains a plural number of pixels. This resulted in very close but inexact values compared to the original plot.

John Kevin Sanchez and Jaime Olivares helped me in acquiring a photocopy of a hand-drawn graph.

References:

1. M. Soriano, A2 – Digital Scanning, Applied Physics 186, National Institute of Physics, 2014.
2. N. Portugal-Dayrit, “The microbiological assay of amino acids in some Philippine legumes,” College of Science, University of the Philippines Diliman, 1956.

Image references:

http://memegenerator.net